Posts

What is Generative Intelligence?

/in /by

Generative intelligence pairs human perception and decision making capabilities of artificial intelligence (AI) with the scientific disciplines of dynamic complexity and perturbation theory, supported by causal deconstruction, to create a systemic and iterative collection of rational and unbiased knowledge that exceeds human intelligence.

Through the applied use of generative intelligence, it becomes possible for machines to automatically monitor an environment and take action to maximize the chance of successfully achieving a set of defined goals. Generative intelligence covers both known patterns, as well as new, unknown patterns that are exposed through mathematical emulation, and may be discovered through sensitivity analysis and stress testing.

The Expansion of Human Intelligence

Ray Kurzweil envisions a future where, “vastly expanded human intelligence (predominantly non biological) spreads through the universe.” To make this future a reality, we need to expand our definition of AI and our means of understanding and creating intelligence.

Despite recent advancements in artificial intelligences, there are still many things humans can easily do, but smart machines cannot. For instance, new situations baffle artificial intelligences because the deep learning they depend upon uses mainly statistical methods to classify patterns using neural networks.

Neural networks memorize classes of things and in most circumstances know when they encounter them again. To expand the capabilities of AI, people have added more layers and more data to neural networks in an attempt to replicate human intelligence. But pattern recognition (exercised on existing structures) alone can never match the cognitive capabilities of humans and its continuous evolution.

As a result, artificial intelligences fail when they encounter an unknown. Pedro Domingos, the author of The Master Algorithm and a professor of computer science at the University of Washington explains, “A self-driving car can drive millions of miles, but it will eventually encounter something new for which it has no experience.”

Gary Marcus, a professor of cognitive psychology at NYU makes clear the gap between human and artificial intelligences, stating, “We are born knowing there are causal relationships in the world, that wholes can be made of parts, and that the world consists of places and objects that persist in space and time. No machine ever learned any of that stuff using backprop[1].”

To match or even exceed the cognitive capabilities of the human brain, it will be important to employ reliable methods that allow machines to map the causal relationship of dynamically complex systems, uncover the factors that will lead to a system singularity[2] and identify the necessary solutions before the event occurs.

Filling the Gap with Generative Intelligence

When creating intelligence, it is clear that some of the data we need will be available using historical information or big data. But some data will be missing because the event has not yet happened and can only be revealed under certain conditions. To expose the missing data, we must use emulation to reproduce the mechanics of various forward-looking scenarios and examine the potential outcomes.

We currently believe perturbation theory may provide the best fit solution to escape the current limits of artificial intelligence and allow us to recover the unknown. Our mathematical emulation platform uses perturbation theory to not only accurately represent system dynamics and predict limits/singularities, but also reverse engineer a situation to provide prescriptive support for risk avoidance.

We have successfully applied perturbation theory across a diverse range of cases from economic, healthcare, and corporate management modeling to industry transformation and information technology optimization. In each case, we were able to determine with sufficient accuracy the singularity point—beyond which dynamic complexity would become predominant and the predictability of the system would become .

Our approach computes three metrics of dynamic complexity and determines the component, link, or pattern that will cause a singularity. It also allows users (humans or machines) to build scenarios to fix, optimize, or push further the singularity point.

Using situational data revealed by the predictive platform, it then becomes possible to create a new class of artificial intelligence, which we call generative intelligence. The goal of generative intelligence is to identify new cases before they occur and determine the appropriate response. These cases are unknowns in statistical methods, which are limited to prediction based on data collected through experience.

A diagnosis definition and remediation that covers both the experience-based knowns and those that were previously unknown can be stored together to allow for the rapid identification of a potential risk with immediate analysis of root causes and proposed remedial actions. A continuous enrichment of case-based knowledge will lead to new systems with the intelligence necessary to outperform any system which is reliant on only the original sources of known, experience-based data.

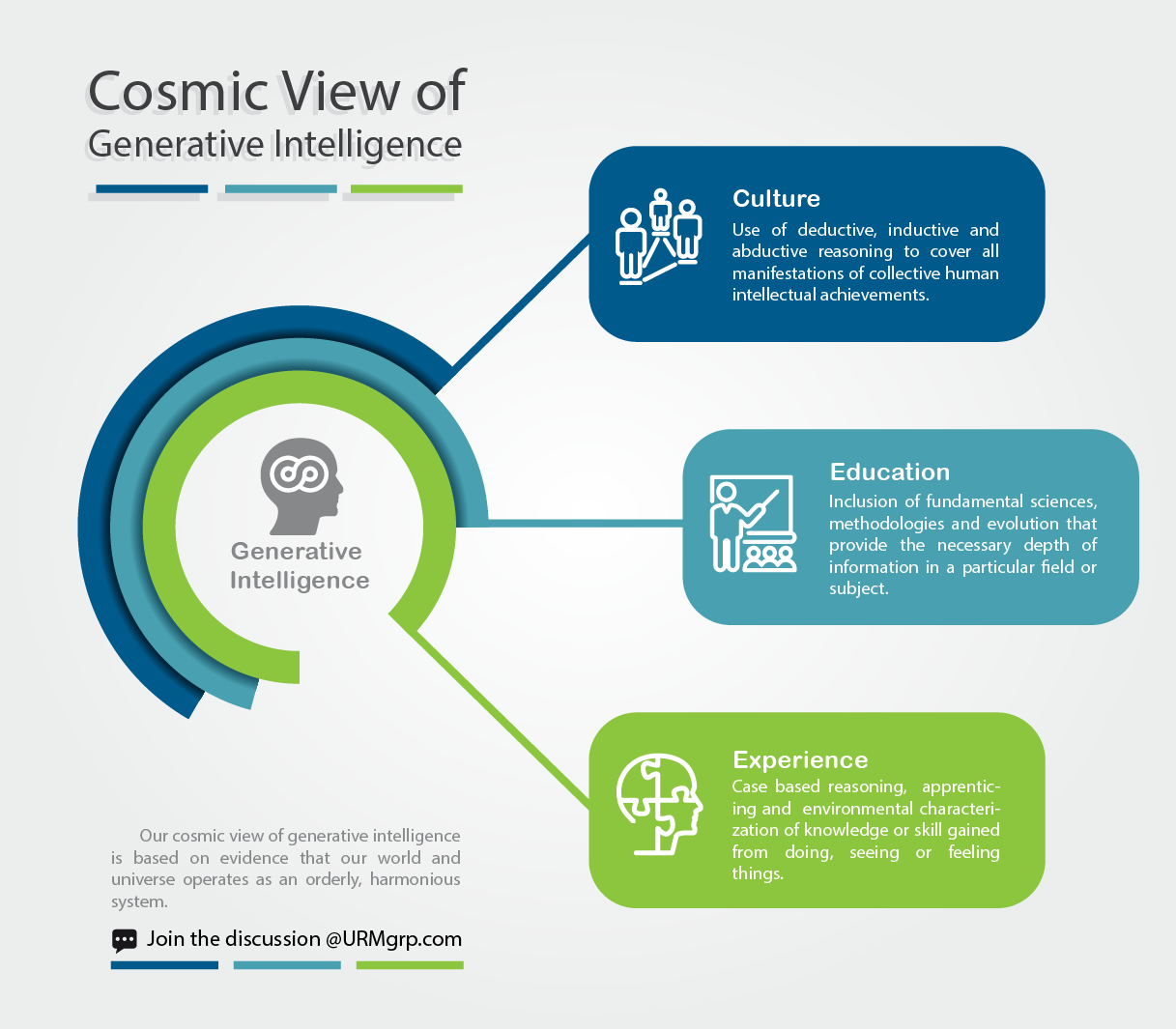
The Cosmic View of Generative Intelligence

We believe systems are deterministic, meaning that their future dynamics are fully defined by their initial conditions and therefore become fully predictable, with no random elements involved. To fully usher in a new era of intelligence and automation, a new culture must be established that will allow machines to extract the knowns but additionally grant them the ability to identify the unknowns.

The only way to achieve this goal is to build machines that are capable of determining the interdependencies and dynamic characteristics that will build gradually, exposing the limitation and identifying the critical zone where dynamic complexity predominates. Through this shift, machines can become adept in employing predictive capabilities to find the weak node of a complex chain through proper sensitivity and stress analysis.

Implementing Generative Intelligence

To accomplish our goal, we must identify all influencing forces. The small influences (considered as outliers by most of today’s popular actual analysis methods) are normally ignored in statistical methods or partial views built from big data relying on past experience that does not necessarily contain the data of attributes, behaviors or situations that have not happened yet. Perturbation theory deals with such attributes and behavior where small divisors and direct and indirect perturbations are involved in the computation regardless of their amplitudes so that all influencing forces are measured and understood. It also enables us to discover situations and predict.

We must also acknowledge outside influencers. The world is open, not in equilibrium, and the Piketty effect[3] adds polarizing forces that make it difficult to derive a conclusion through simple extrapolation. The emulation approach we use computes each prediction based on the parameters involved in the expression of dynamic complexity regardless of the past experience or past collected big data and therefore will produce projections independent from the analytical conditions an approach may impose—closed vs. open, or equilibrium vs. reactive/deterministic.

In this way, generative intelligence can be constructed based on a mix human experience, algorithms, observations, deductive paradigms and long range discoveries and notions that were previously considered external such as perception, risk, non-functional requirements (NFRs) and cost vs. benefits. Additionally, the sophistication of intelligence will independently evolve through a continuous process of renewal, adaption, and enrichment.

Managing the Move to the Cognitive Era

We see generative intelligence as the synthesis for the human progress. It escapes the taboos and congestion caused by past artificial intelligence philosophies and frees the human potential by using rational and unbiased mechanisms to harness the technological advances of the Fourth Industrial Revolution to create intelligent machine systems capable of predicatively, self-diagnosing problems and preventively, applying self-healing actions. In the simplest of terms, generative intelligence is able to continuously evolve by adding new intelligence that may not have been obvious at the outset.

Accomplishing such an ambitious goal will require new education and training, as well as a transfer of knowhow and scientific foundations. Additionally, we must anticipate the possible repercussions and enforce the ethics necessary to manage labor, inequality, humanity, security and other related risks. This level of technological progress has the potential to benefit all of humanity, but only if we implement it responsibly.

[1] Backprop or Backpropagation, short for “backward propagation of errors,” is an algorithm for supervised learning of artificial neural networks using gradient descent. Given an artificial neural network and an error function, the method calculates the gradient of the error function with respect to the neural network’s weights. It is a generalization of the delta rule for perceptrons to multilayer feedforward neural networks.

[2] We restrict our use of the term singularity to the one that defines the mathematical singularity as a point at which a given mathematical object is not defined or not well behaved, for example infinite or not differentiable.

[3] Piketty, Thomas. Capital in the 21st Century. Trans. Arthur Goldhammer. N.p.: Harvard UP, 2014. Print.

Using X-ACT Metrics to Guide Decisions

/in /by

Learn how to make operational risk decisions with confidence

The X-ACT: Using Metrics to Guide Decisions | How to Guide shows how companies use the advanced analytics and emulation capabilities supported by X-ACT to identify how dynamic complexity leads to system limits, diagnose the root cause of limits and determine the best remedial actions by weighing the benefits, complexity and cost of proposed solutions.

Download Guide

The analytics and emulation capabilities supported by X-ACT® arm business and technology leaders worldwide with the foresights they need to confidently respond to changing system dynamics and clearly understand which (and when) preventive and opportunistic actions should be taken to ensure the continuous efficiency and cost effectiveness of operations.

Using accurate, representative and reproducible models of business processes, applications and infrastructure, X-ACT delivers an end-to-end emulation of a service that accurately represents the behavior of system dynamics. The emulation replaces structures, characteristics and behaviors by perturbations exerted on dynamic equations through multiple order perturbations on dynamic coordinates such as volume, service quality and cost. This is very complex math, but it is handled entirely by X-ACT.

Once a system is transformed into an emulation, it allows users to quickly test and economically explore an unlimited number of scenarios that would otherwise be complex, expensive or even impossible to test on a real system. In comparison to other practices, such as simulation, emulation is superior in its ability to accurately replicate a system, but its biggest advantage is that it allows for the discovery of previously unknown patterns, which cannot be determined using any other method.

Now users can emulate risk because X-ACT can mathematically reproduce unknowns that may happen under certain conditions. Once the emulation process is complete, X-ACT users can change variables—such as volume, architecture and infrastructure or perform sensitivity predictions on changing process dynamics—to observe the outcomes (even when we have no historical record of these events ever happening).

Discovering the cause and effects of dynamic complexity is foundational to our universal risk management approach. Since conventional methods ignore the unknowns, risk often appears as a surprise that may potentially impact operational performance. To predict risk and anticipate the appropriate course of treatment, we must discover these unknowns and determine their current and future influence on system behavior.

The X-ACT: Using Metrics to Guide Decisions | How to Guide shows how companies use the advanced analytics and emulation capabilities supported by X-ACT to identify risk and take remedial actions by weighing the benefits, complexity and cost of available solutions.

New Book from Dr. Abu el Ata Offers A New Framework to Predict, Remediate and Monitor Risk

/in /by

“The Tyranny of Uncertainty” is now available for purchase on Amazon.com

Omaha, NE—May 18, 2016–Accretive Technologies, Inc. (Accretive) announces the release of a new book, “The Tyranny of Uncertainty.” Accretive Founder and CEO, Dr. Nabil Abu el Ata, jointly authored the book with Rudolf Schmandt, Head of EMEA and Retail production for Deutsche Bank and Postbank Systems board member, to expose how dynamic complexity creates business risks and present a practical solution.

The Tyranny of Uncertainty explains why traditional risk management methods can no longer prepare stakeholders to act at the right time to avoid or contain risks such as the Fukushima Daiichi Nuclear Disaster, the 2007-2008 Financial Crisis, or Obamacare’s Website Launch Failure. By applying scientific discoveries and mathematically advanced methods of predictive analytics, the book demonstrates how business and information technology decision makers have used the presented methods to reveal previously unknown risks and take action to optimally manage risk.

Further, the book explains the widening impact of dynamic complexity on business, government, healthcare, environmental and economic systems and forewarns readers that we will be entering an era chronic crisis if the appropriate steps are not taken to modernize risk management practices. The presented risk management problems and solutions are based upon Dr. Abu el Ata’s and Mr. Schmandt’s decades of practical experience, scientific research, and positive results achieved during early stage adoption of the presented innovations by hundreds of global organizations.

The book is available  to order on amazon.com at https://www.amazon.com/Tyranny-Uncertainty-Framework-Predict-Remediate/dp/3662491036/ref=sr_1_1.

The methodologies and innovations presented in this book by Dr. Abu El Ata and Mr. Schmandt are now in various stages of adoption with over 350 businesses worldwide and the results have been very positive. Businesses use the proposed innovations and methodologies to evaluate new business models, identify the root cause of risk, re-architect systems to meet business objectives, identify opportunities for millions of dollars of cost savings and much more.

About Accretive

Accretive Technologies, Inc. offers highly accurate predictive and prescriptive business analytic capabilities to help organizations thrive in the face of increasing pressures to innovate, contain costs and grow. By leveraging the power of Accretive’s smart analytics platform and advisory services, global leaders in financial, telecommunications, retail, entertainment, services and government markets gain the foresight they need to make smart transformation decisions and maximize the performance of organizations, processes and infrastructure. Founded in 2003 with headquarters in New York, NY and offices in Omaha, NE and Paris, France, Accretive is a privately owned company with over 350 customers worldwide. For more information, please visit http://www.acrtek.com.

Perturbation Theory

/in /by

Perturbation theory provides a mathematical method for finding an approximate solution to a problem, by starting from the exact solution of a related problem. A critical feature of the technique is a middle step that breaks the problem into “solvable” and “perturbation” parts. Perturbation theory is applicable if the problem at hand cannot be solved exactly, but can be formulated by adding a “small” term to the mathematical description of the exactly solvable problem.

Background

Perturbation theory supports a variety of applications including Poincaré’s chaos theory and is a strong platform to deal with the dynamic behavior problems . However, the success of this method is dependent on our ability to preserve the analytical representation and solution as far as we are able to afford (conceptually and computationally). As an example, I successfully applied these methods in 1978 to create a full analytical solution for the three-body lunar problem[1].

In 1687, Isaac Newton’s work on lunar theory attempted to explain the motion of the moon under the gravitational influence of the earth and the sun (known as the three-body problem), but Newton could not account for variations in the moon’s orbit. In the mid-1700s, Lagrange and Laplace advanced the view that the constants, which describe the motion of a planet around the Sun, are perturbed by the motion of other planets and vary as a function of time. This led to further discoveries by Charles-Eugène Delaunay (1816-1872), Henri Poincaré (1854 – 1912), and more recently I used predictive computation of direct and indirect planetary perturbations on lunar motion to achieve greater accuracy and much wider representation. This discovery has paved the way for space exploration and further scientific advances including quantum mechanics.

How Perturbation Theory is Used to Solve a Dynamic Complexity Problem

The three-body problem of Sun-Moon-Earth is an eloquent expression of dynamic complexity whereby the motion of planets are perturbed by the motion of other planets and vary as a function of time. ‪ While we have not solved all the mysteries of our universe, we can predict the movement of a planetary body with great accuracy using perturbation theory.

During my doctorate studies, I found that while Newton’s law is ostensibly true in a simple lab setting, its usefulness decreases as complexity increases. When trying to predict the trajectory (and coordinates at a point in time) of the three heavenly bodies, the solution must account for the fact that the gravity attracts these bodies to each other depending on their mass, distance, and direction. Their path or trajectory therefore undergoes constant minute changes in velocity and direction, which must be taken into account at every step of the calculation. I found that the problem was solvable using common celestial mechanics if you start by taking only two celestial bodies, e.g. earth and moon.

But of course the solution is not correct because the sun was omitted from the equation. So this incorrect solution is then perturbed by adding the influence of the sun. Note that the result is modified, not the problem, because there is no formula for solving a problem with three bodies. Now we are closer to reality but still far from precision, because the position and speed of the sun, which we used was not its actual position. Its actual position is calculated using the same common celestial mechanics as above but applied this time to the sun and earth, and then perturbing it by the influence of the moon, and so on until an accurate representation of the system is achieved.

Applicability to Risk Management

The notion that the future rests on more than just a whim of the gods is a revolutionary idea. A mere 350 years separate today’s risk-assessment and hedging techniques from decisions guided by superstition, blind faith, and instinct. During this time, we have made significant gains. We now augment our risk perception with empirical data and probabilistic methods to identify repeating patterns and expose potential risks, but we are still missing a critical piece of the puzzle. Inconsistencies still exist and we can only predict risk with limited success. In essence, we have matured risk management practices to the level achieved by Newton, but we cannot yet account for the variances between the predicted and actual outcomes of our risk management exercises.

This is because most modern systems are dynamically complex—meaning system components are subject to the interactions, interdependencies, feedback, locks, conflicts, contentions, prioritizations, and enforcements of other components both internal and external to the system in the same way planets are perturbed by other planets. But capturing these influences either conceptually or in a spreadsheet is impossible, so current risk management practices pretend that systems are static and operate in a closed-loop environment. As a result, our risk management capabilities are limited to known risks within unchanging systems. And so, we remain heavily reliant on perception and intuition for the assessment and remediation of risk.

I experienced this problem first hand as the Chief Technology Officer of First Data Corporation, when I found that business and technology systems do not always exhibit predictable behaviors. Despite the company’s wealth of experience, mature risk management practices and deep domain expertise, sometimes we would be caught off guard by an unexpected risk or sudden decrease in system performance. And so I began to wonder if the hidden effects which made the prediction of satellite orbits difficult, also created challenges in the predictable management of a business. Through my research and experiences, I found that the mathematical solution provided by perturbation theory was universally applicable to any dynamically complex system—including business and IT systems.

Applying Perturbation Theory to Solve Risk Management Problems

Without the ability to identify and assess the weight of dynamic complexity as a contributing factor to risk, uncertainty remains inherent in current risk management and prediction methods. When applied to prediction, probability and experience will always lead to uncertainties and prohibit decision makers from achieving the optimal trade-off between risk and reward. We can escape this predicament by using the advanced methods of perturbation mathematics I discovered as computer processing power has advanced sufficiently to support my methods perturbation based emulation to efficiently and effectively expose dynamic complexity and predict its future impacts.

Emulation is used in many industries to reproduce the behavior of systems and explore unknowns. Take for instance space exploration. We cannot successfully construct and send satellites, space stations, or rovers into unexplored regions of space based merely on historical data. While the known data from past endeavors is certainly important, we must construct the data which is unknown by emulating the spacecraft and conducting sensitivity analysis. This allows us to predict the unpredicted and prepare for the unknown. While the unexpected may still happen, using emulation we will be better prepared to spot new patterns earlier and respond more appropriately to these new scenarios.

Using Perturbation Theory to Predict and Determine the Risk of Singularity

Perturbation theory seems to be the best-fit solution for providing accurate formulation of dynamic complexity that is representative of the web of dependencies and inequalities. Additionally, perturbation theory allows for predictions that correspond to variations in initial conditions and influences of intensity patterns.  In a variety of scientific areas, we have successfully applied perturbation theory to make accurate predictions.

After numerous applications of perturbation theory based-mathematics, we can affirm its problem solving power. Philosophically, there exists a strong affinity between dynamic complexity and its discovery revealed through perturbation based-solutions. At the origin, we used perturbation theory to solve gravitational interactions. Then we used it to reveal interdependencies in mechanics and dynamic systems that produce dynamic complexity. We feel strongly that perturbation theory is the right foundational solution of dynamic complexity that produces a large spectrum of dynamics: gravitational, mechanical, nuclear, chemical, etc. All of them represent a dynamic complexity dilemma. All of them have an exact solution if and only if all or a majority of individual and significant inequalities are explicitly represented in the solution.

An inequality is the dynamic expression of interdependency between two components. Such dependency could be direct (e.g. explicit connection always first order) or indirect (connection through a third component that may be of any order on the base that the perturbed perturbs). As we can see, the solutions based on Newton’s work were only approximations of reality as Newton principles considered only the direct couples of interdependencies as the fundamental forces.

We have successfully applied perturbation theory across a diverse range of cases from economic, healthcare, and corporate management modeling to industry transformation and information technology optimization. In each case, we were able to determine with sufficient accuracy the singularity point—beyond which dynamic complexity would become predominant and the predictability of the system would become chaotic.

Our approach computes the three metrics of dynamic complexity and determines the component, link, or pattern that will cause a singularity. It also allows users to build scenarios to fix, optimize, or push further the singularity point. It is our ambition to demonstrate clearly that perturbation theory can be used to not only accurately represent system dynamics and predict its limit/singularity, but also to reverse engineer a situation to provide prescriptive support for risk avoidance.

More details on how we apply perturbation theory to solve risk management problems and associated case studies are provided in my book, The Tyranny of Uncertainty.

[1] Abu el Ata, Nabil. Analytical Solution the Planetary Perturbation on the Moon. Doctor of Mathematical Sciences Sorbonne Publication, France. 1978.

 

Understanding Dynamic Complexity

/in /by

Complexity is a subject that everyone intuitively understands. If you add more components, more requirements or more of anything, a system apparently becomes more complex. In the digital age, as globalization and rapid technology advances create an ever-changing world at a faster and faster pace, it would be hard not to see the impacts of complexity, but dynamic complexity is less obvious. It lies hidden until the symptoms reveal themselves, their cause remaining undiscovered until their root is diagnosed. Unfortunately, diagnosis often comes too late for proper remediation. We have observed in the current business climate that the window of opportunity to discover and react to dynamic complexity and thereby avoid negative business impacts is shrinking.

Dynamic Complexity Defined

Dynamic complexity is a detrimental property of any complex system in which the behaviorally determinant influences between its constituents change over time. The change can be due to either internal events or external influences. Influences generally occur when a set of constituents (1…n) are stressed enough to exert an effect on a dependent constituent, e.g. a non-trivial force against a mechanical part, or a delay or limit at some stage in a process. Dynamic complexity creates what was previously considered unexpected effects that are impossible to predict from historic data—no matter the amount—because the number of states tends to be too large for any given set of samples.

Dynamic complexity—over any reasonable period of time—always produces a negative effect (loss, time elongation, or shortage), causing inefficiencies and side effects, similar to friction, collision or drag. Dynamic complexity cannot be observed directly, only its effects can be measured.

Static vs. Dynamic Complexity

To understand the difference between complexity (a.k.a. static complexity) and dynamic complexity, it is helpful to consider static complexity as something that can be counted (a number of something), while dynamic complexity is something that is produced (often at a moment we do not expect). Dynamic complexity is formed through interactions, interdependencies, feedback, locks, conflicts, contentions, prioritizations, enforcements, etc. Subsequently, dynamic complexity is revealed through forming congestions, inflations, degradations, latencies, overhead, chaos, singularities, strange behavior, etc.

Human thinking is usually based on linear models, direct impacts, static references, and 2-dimensional movements. This reflects the vast majority of our universe of experiences. Exponential, non-linear, dynamic, multi-dimensional, and open systems are challenges to our human understanding. This is one of the natural reasons we can be tempted to cope with simple models rather than open systems and dynamic complexity. But simplifying a dynamic system into a closed loop model doesn’t make our problems go away.

Dynamic Complexity Creates Risk

With increasing frequency, businesses, governments and economies are surprised by a sudden manifestation of a previously unknown risk (the Fukushima Daiichi Nuclear Disaster, the 2007-2008 Financial Crisis, or Obamacare’s Website Launch Failure are a few recent examples). In most cases the unknown risks are caused by dynamic complexity, which lies hidden like a cancer until the symptoms reveal themselves.

Often knowledge of the risk comes too late to avoid negative impacts on business outcomes and forces businesses to reactively manage the risk. As the pace of business accelerates and decision windows shrink, popular methods of prediction and risk management are becoming increasingly inadequate. Real-time prediction based on historical reference models is no longer enough.  To achieve better results, businesses must be able to expose new, dangerous patterns of behavior with sufficient time to take corrective actions—and be able to determine with confidence which actions will yield the best results.

 

Dynamic Complexity’s Role in 2007-2008 Financial Crisis

/in , /by

After the economic events of 2007 and 2008, many economic experts claimed that they had predicted that such a disaster would occur, but none were able to preemptively pinpoint the answers to key questions that would have helped us prepare for such an event or even lessen its impacts, including: When will it occur? What will be the cause? How will it spread? And, how wide will its impacts be felt?

The then-U.S. Treasury Secretary, Henry Paulson, recognized that the credit market boom obscured the real danger to the economy.  Despite all the claims of knowing the true triggers of the economic recession, we believe the importance of dynamic complexity has been overlooked in everyone’s analysis. The real cause of the economic meltdown can be traced to intertwined financial domains, which generated considerable dynamic complexity that in turn made it difficult to determine the possible outcomes. There is no doubt that the subprime foreclosure rate started the domino effect, but had the degree of inter-domains dependency not pre-existed, then the effect on the market would have been much less severe.

While some seasoned experts have alluded to the same conclusion, most have considered that the market complexity (in a broad and immeasurable sense) played a significant role in creating the risk, which ultimately caused a global recession. But most conclude that the aggregate risk of complexity was not necessarily something that the market should be able to predict, control and mitigate at the right time to avoid the disaster.

While dynamic complexity can be identified after the fact as the origin of many unknowns that ultimately lead to disaster, most financial services and economic risk management models accept market fluctuations as something that is only quantifiable based on past experience or historical data.  However, the next economic shock will come from a never-seen-before risk. And the distance between economic shocks will continue to shrink as banks add more technology and more products/services, further compounding the inherent risk of dynamic complexity.

A Better Path Forward

Revealing the unknowns through the joint power of deconstruction theory and mathematical perturbation theory allows for both the determination of potential cause origins (allowing the evolution to happen as reactions to the influencer’s changes) and helps to predict the singularity/chaos point and the distance to such point in time.  As we privilege the determinism, we consider that any observation points to a cause and that such a cause should be discovered by the tools we possess. Openly, we are trying to convince you that, “If we know the cause, then we will be able to predict when it will occur, the severity of risk and what may be the amplitude of a possible singularity.” This will then afford us the time needed to mitigate the risk.


Figure 1. Spread between 3-month LIBOR and 3-month Expected Federal Funds Rate (January 2007 – May 2008 daily)

By reviewing graphs of the financial market from 2007 to 2008, we discovered that market changes happened at the vertices as well as at the edges, as we would normally expect. The example in Figure 1 illustrates part of the story.

According to Stephen G. Cecchetti[1], the divergence between the two rates is typically less than 10 basis points. This small gap arises from an arbitrage that allows a bank to borrow at LIBOR (London Interbank Offer Rate), lend for three months, and hedge the risk that the comparable overnight index swap rates (OIS) will move in the federal funds futures market, leaving only a small residual level of credit and liquidity risk that accounts for the usually small spread. But on August 9, 2007, the divergence between these two interest rates jumped to 40 basis points.

The problem lies in the worst case. Each vitric and each edge directly connects to every other vitric and every other edge, and therefore represents the direct effects covered by perturbation theory as presented in Figure 29.2. But, because each one is perturbed, the analysis will not be sufficient to understand the full picture if we do not add the indirect effects on the direct ones. This points precisely to the difference between Paulson’s analysis and ours.

 

Figure 2. Schematic Representation of Financial Market Dependencies and Crisis Points

In short, Paulson attributed the crisis to the housing bubble and we attribute it to the dynamic complexity, which includes multiple dependencies within the whole market: housing market, equity, capital market, corporate health, and banking solvency, which in turn impacted the money supply that caused massive unemployment and severe recession.

A major result of our analysis was still not obvious or entirely elucidated when Henry Paulson expressed his own analysis. Indeed, the housing bubble precipitated the crisis, but the real cause was a large proportion of dynamic complexity that was hidden in the overall construct of the financial system. This means that any regulation, organization, and consequently, surveillance of the system should measure the impact of dynamic complexity, if we hope to adequately predict and mitigate its risk.

[1] Cecchetti, Stephen G. Crisis and Responses: The Federal Reserve in the Early Stages of the Financial Crisis. Journal of Economic Perspectives, American Economic Association, vol. 23(1), pages 51-75, Winter 2009. PDF file.

 

Portfolio Items